XAI for Transformers. Explanations through LRP #

Introduction #

Transformers are becoming more and more common these days. But transformers are based on DNN that makes it harder to explain than other models. However, more and more ordinary users are starting to work with LLMs and to have more questions and doubts for its’ work and decisions. Thus, there is a need for some explanation of Transformers. The method presented in the article “XAI for Transformers: Better Explanations through Conservative Propagation” by Ameen Ali et. al. serves this purpose.

LRP method #

Layer-wise Relevance Propagation method here are compared with Gradient×Input method presented in earlier article in this field.

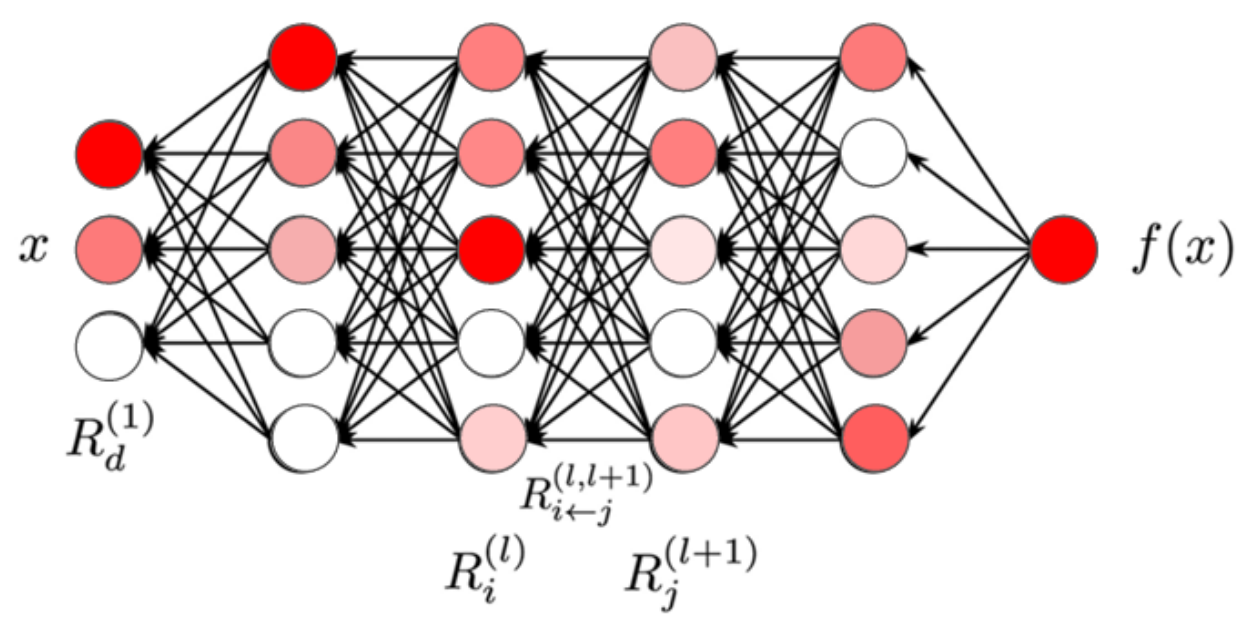
LRP outlook

Img.1. Layer-wise Relevance Propagation principe

The relevence in LRP is computing as $$R(x_i) = \sum_{j} \frac{\delta y_j}{\delta x_i} \frac{x_i}{y_j} R(y_j)$$

But in some layers of transformer formulas look little different. For the attention-head layer and for normalization layers rules are look like

\[R(x_i)=\sum_{j}\frac{x_i p_ij}{\sum_{i'} x_{i'} p_{i'j}}R(y_j) \text{ and } R(x_i)=\sum_{j}\frac{x_i (\delta_{ij} - \frac{1}{N})}{\sum_{i'} x_{i'} (\delta_{i'j} - \frac{1}{N})}R(y_j),\]

where $p_{ij}$ is a gating term value from attention head and for the LayerNorm $(\delta_{ij} - \frac{1}{N})$ is the other way of writing the ‘centering matrix’, $N$ is the number of tokens in the input sequence.

Better LRP Rules for Transformers #

In practice authors observed that these rules do not need to be implemented explicitly. There are trick makes the method straightforward to implement, by adding detach() calls at the appropriate locations in the neural network code and then running standard Gradient×Input.

So improved rules will be \[y_i = \sum_i x_i[p_{ij}].detach()\] for every attention head, and \[y_i = \frac{x_i - \mathbb{E}[x]}{\sqrt{\varepsilon + Var[x]}}.detach()\] for every LayerNorm, where $ \mathbb{E}$ and $Var[x]$ is mean and variance.

Results #

In the article different methods was tested on various datasets, but for now most inetersing is comparisom between old Gradient×Input (GI) method and new LRP methods with modifications in attention head rule (AH), LayerNorm (LN) or both (AH+LN).

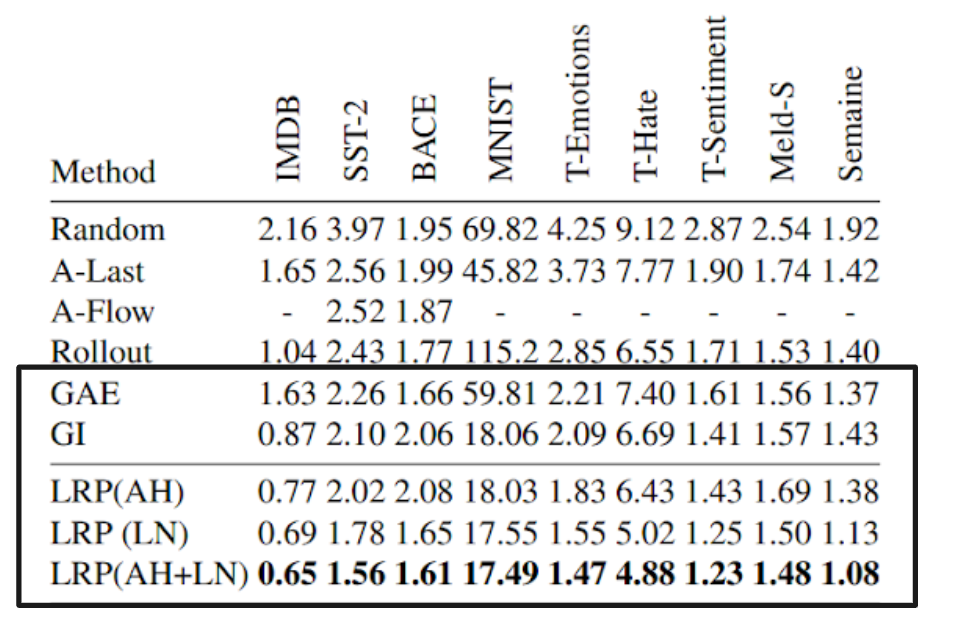
GIvsLRP results

Img.2. AU-MSE (area under the mean squared error)

The LRP with both modifications shows slightly better results in comparison with Gradient×Input method, but may make a huge difference in the future.

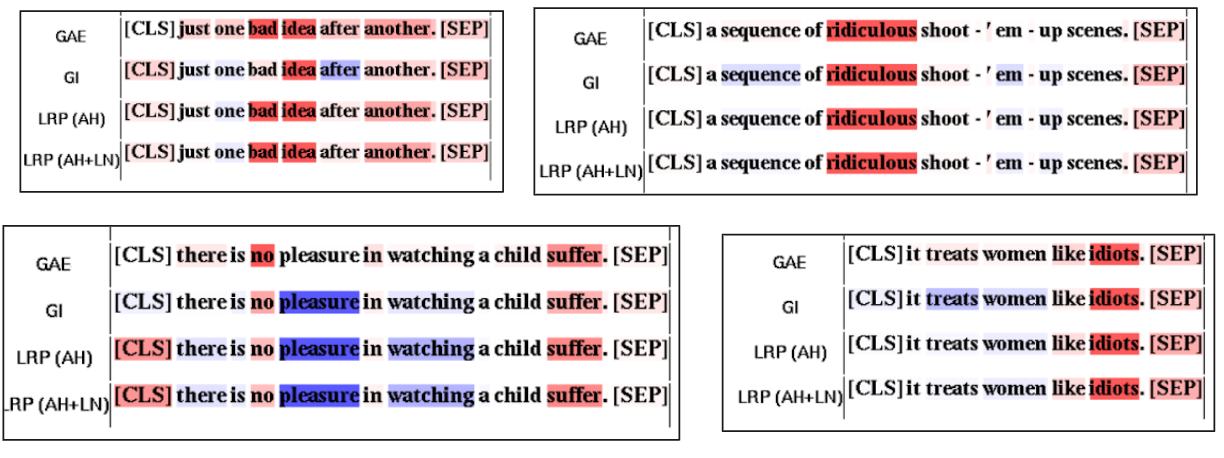
The results on SST-2 dataset that contains movie reviews and ratings are shown below. Both transformers was learned to classify review as positive or negative, and LRP shows slightly brighter and more concrete relevance values.

SST-2 results

References #

[1] Ameen Ali et. al. “XAI for Transformers: Better Explanations through Conservative Propagation.” ICML, 2022

[2] Hila Chefer et. al. “Transformer Interpretability Beyond Attention Visualization.” CVPR, 2021

Code #

All code for Transformer you can find in https://github.com/AmeenAli/XAI_Transformers